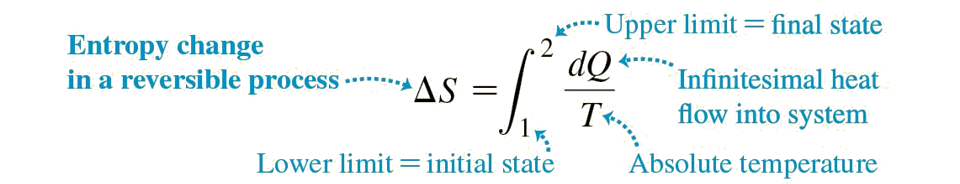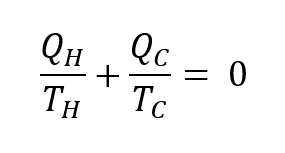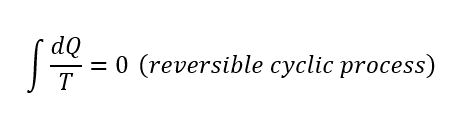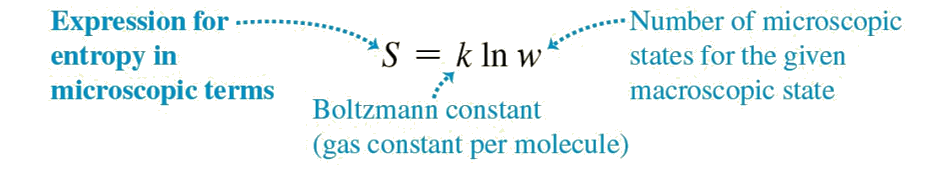Entropy
The second law is nothing more than a statement which determines the impossiblity of an event. It is not a mathemtical equation or a quantative relationship. It is just a conceptual basis for understanding the directions of thermodynamics events. However, by using entropy, the second law can be restated as a quantative relationship.
There are several relationships which the entropy is taken into account differently such as entropy in reversible processes, in cyclic processes etc. They are all same in principle but as in the definitions of the second law, they can be used for differrent applications.
We will cover these and such relationships one by one.
Entropy in Reversible Processes
Remember, this equation is only valid for reversible processes.
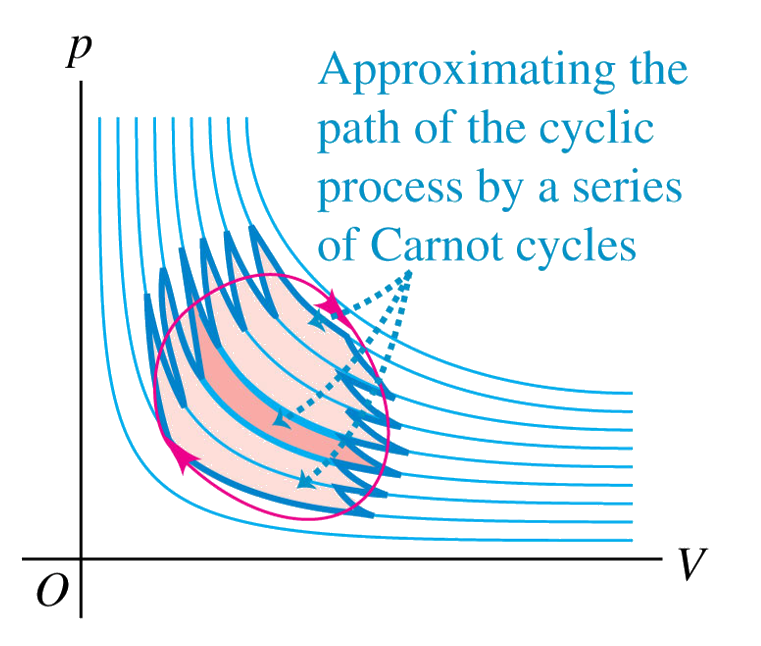
Entropy in Cyclic Processes
Since, the work and the heat are the same in a cyclic process, it can easily be shown that,
The first term in the equation above is equal to the change in entropy which occurs at T = TH. By using the same logic, the second term is equal to the change in entropy at T = TC. So,
the total entropy change is zero in a cycle. This equation is also valid for the Carnot cycle because we know that the efficiencies of any Carnot engine that are operating between same temperatures are the same. If you combine this information and the equation above, you can easily see that the net entropy change is zero.
More general,
Entropy in Irreversible Processes
It was not like as in reversible processes. In reversible processes as I mentioned before the processes are just equilbrium processes. Thus, the total entropy change of the system and its surroundings is zero. However, in real systems, irreversible systems, entropy can change. As I mentioned before, entropy of a closed system can only increase or remain the same but never decrease.
Entropy and the Second Law
When we take all the systems into account, the entropy change is not like in reversible processes. The second law states that energy has quality as well as quantity. All the real systems occur in the direction of decreasing quality. That means, the entropy can only increase or remain same in a real thermodynamic event. This statement equals to the engine and the refrigerator statements. I hope you get the feeling that increasing entropy means increasing randomness in the universe. If you do not understand it yet, check the topic below which will give you a insight of what that all means.
MICROSCOPIC INTERPRETATION OF ENTROPY
Entropy is a concept that has many definitions, constitutes the theoretical basis for answering many of the questions we ask about the universe and is both very easy and very difficult to understand. Entropy, by one of its definitions, is a measure of disorder and is directly related to the second law of thermodynamics. By virtue of this law, entropy in closed systems always increases or remains constant. From a deeper perspective, entropy relates to Ludwig Boltzmann’s definition which is the naturel logarithm of the number of microscopic states that you can change without changing the macroscopic structure of a system.
It can be explained with a simple thought experiment. Imagine a box which is split with a compartment at the very middle of it. There is a passage of the compartment that connects the two sides of the box. In the first case, let’s start with a system where we assume that there are 2000 gas molecules on one side of the box and 0 on the other side. After a certain period, as we have foreseen in our daily experience, the box will be able to have around 1000 molecules on either side thanks to the transition region. In this case, at the very beginning of the transition, there is only 1 possibility that all the gas molecules in the one side of the box.
W = 1, logW = 0; S1 = k.logW = 0
By the time passes, the box tries to equalize the number of the gas molecules on each side. There are 2000 possibilities to have 1 molecule on one side and 1999 on the other (each gas molecule may be on the one-particle side, 2000 possibilities for 2000 molecules.
W = 2000, logW = 3.3; S2 >S1
It is seen that the entropy increases with the statistical analysis of the passage of the molecules to the other side of the box. In the case of 1000 molecules on both sides, the naturel logarithm of the number of micro-states formed by the interchangeability of each molecule is about 600.
W = (2000! - 1000!)/1000! ~ 2 x 10600; logW = 600.log2; S1000 >>S1
That is, the probability that the particles are evenly distributed on both sides in the box is 200…000 (600 zeros after 2) more than the probability for all particles to accumulate on one side. This is also the reason why it is easy to mix milk and coffee, but it is difficult to separate the mixed milk coffee, and it is also the reason why a broken egg cannot return to its unbroken state itself. For any system in the universe, high entropy is more likely than low. You can test it in every aspect of your life and see that entropy always tends to increase or remain constant when you allow the necessary time to pass. For example, we can remember the past and build memories we trust, but we can only make predictions about the future. That is because the entropy is lower in the past and higher in the future. As you would expect, there is more possibility for your future, but not for your past. You can create precise memories of your low entropy (low probability) past, transfer them, and mutually verify your memories with your stakeholders.
That is the end of the this section. I hope that will be useful for your work. If you have any problem with the usage of the website, the informations in the website or any problem that may occur, you can contact me without hesitation by using the e-mail address below. Also, you can find useful resources in the next section.
Videos and Readings